Шановні учні!
Даний довідник може стати вам у пригоді для розв'язку задач
Введення цілих чисел:
Якщо вам треба ввести ціле число від користувача в вашу програму, то використовуйте конструкцію:
x = int(input())
Якщо вам треба ввести два цілих числа, кожне з яких записане в окремому рядку, то це можна зробити так:
x = int(input())
y = int(input())
Якщо вам треба ввести в вашу програму кілька цілих чисел, що записані через пропуск, то це можна зробити так:
a, b, c = map(int, input().split())
Введення дійсних чисел:
Якщо вам треба ввести дійсне число від користувача в вашу програму, то використовуйте конструкцію:
x = float(input())
Якщо вам треба ввести в вашу програму кілька дійсних чисел, що записані через пропуск, то це можна зробити так:
a, b, c = map(float, input().split())
Введення тексту:
Якщо вам треба ввести текст від користувача в вашу програму то використовуйте таку конструкцію:
x = input()
Якщо вам треба ввести текст від користувача в вашу програму, при цьому обрізати пропуски на початку тексту і в кінці, то використовуйте таку конструкцію:
x = input().strip()
Пам'ятайте, що з текстом не можна проводити математичні операції. З тексту ви можете вирізати один або кілька символів, і вирізана частина буде також текстом. Якщо ж вам треба виконати математичні дії з цими даними, то треба конвертувати текст в число. Якщо це стосується цілих чисел, то конструкція така:
y = int(x)
Приклад обчислення квадратного кореня:
import math
x = math.sqrt(4)
print(x)
Виведення даних:
Для виведення даних використовується оператор print()
Приклад виведення тексту:
print('Страшно хочу в школу!')
Приклад виведення числа:
a = 5
b = 3
print(a-b)
Для виведення дійсного числа з певною кількістю знаків після коми можна скористатися f-рядками.
Приклад: Треба вивести дійсне число з трьома знаками після коми:
x = 12.34567
print(f"{x:.3f}")
Розгалуження:
Задача для прикладу:
Програма повинна прочитати від користувача ціле число та вивести -1, 0 або 1, якщо введене значення від’ємне, нульове і додатне, відповідно.
Приклад коду:
n = int(input())
if n < 0:
print(-1)
elif n == 0:
print(0)
else:
print(1)
Цикл FOR:
Задача для прикладу:
Програма повинна прочитати від користувача ціле число та вивести числа від одиниці до цього числа включно. Кожне число - в окремому рядку.
Приклад коду:
n = int(input())
for x in range(1, n + 1):
print(x)
Задача для прикладу:
Програма повинна прочитати від користувача ціле число та вивести числа від цього числа до нуля в порядку зменшення. Кожне число - в окремому рядку.
Приклад коду:
n = int(input())
for x in range(n, - 1, -1):
print(x)
Якщо це саме треба зробити так, щоб всі числа були в одному рядку, ось приклад:
n = int(input())
for x in range(n, - 1, -1):
print(x, end = ' ')
Розбираємо задачу з 8545 з e-olimp під назвою «Таблиця множення».
https://www.e-olymp.com/uk/problems/8545
Проста задача, в принципі. Знову таки, з дивно високим коефіцієнтом складності, 21%. Треба побудувати квадратну матрицю, як на обкладинках зошитів з математики. Вхідні дані - розмірність матриці, від 1 до 9 включно. Результат відповідним чином відформатувати:
n = 5
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
5 10 15 20 25
n = 7
1 2 3 4 5 6 7
2 4 6 8 10 12 14
3 6 9 12 15 18 21
4 8 12 16 20 24 28
5 10 15 20 25 30 35
6 12 18 24 30 36 42
7 14 21 28 35 42 49
Запропонував Саша цю задачу. З приміткою «неробіт». Проходить 70% тестів. E-olimp, на відміну від codeforces, тести не відкриває, шукаємо помилку аналітично.
Показав Саша код:
a = int(input())
if a == 1:
print( '1')
elif a == 2:
print(' 1 2\n 2 4')
elif a == 3:
print(' 1 2 3 \n 2 4 6 \n 3 6 9')
elif a == 4:
print(' 1 2 3 4 \n 2 4 6 8 \n 3 6 9 12 \n 4 8 12 16')
elif a == 5:
print(' 1 2 3 4 5 \n 2 4 6 8 10 \n 3 6 9 12 15 \n 4 8 12 16 20 \n 5 10 15 20 25')
elif a == 6:
print(' 1 2 3 4 5 6 \n 2 4 6 8 10 12 \n 3 6 9 12 15 18 \n 4 8 12 16 20 24 \n 5 10 15 20 25 30 \n 6 12 18 24 30 36')
elif a == 7:
print(' 1 2 3 4 5 6 7 \n 2 4 6 8 10 12 14 \n 3 6 9 12 15 18 21 \n 4 8 12 16 20 24 28 \n 5 10 15 20 25 30 35 \n 6 12 18 24 30 36 42 \n 7 14 21 28 35 42 49')
elif a == 8:
print(' 1 2 3 4 5 6 7 8 \n 2 4 6 8 10 12 14 16 \n 3 6 9 12 15 18 21 24 \n 4 8 12 16 20 24 28 32 \n 5 10 15 20 25 30 35 40 \n 6 12 18 24 30 36 42 48 \n 7 14 21 28 35 42 49 56 \n 8 16 24 32 40 48 56 64')
else:
print(' 1 2 3 4 5 6 7 8 9 \n 2 4 6 8 10 12 14 16 18 \n 3 6 9 12 15 18 21 24 27 \n 4 8 12 16 20 24 28 32 36 \n 5 10 15 20 25 30 35 40 45 \n 6 12 18 24 30 36 42 48 54 \n 7 14 21 28 35 42 49 56 63 \n 8 16 24 32 40 48 56 64 72 \n 9 18 27 36 45 54 63 72 81 ')
Звичайно, Саша дізнався про себе багато цікавого після оприлюднення такого щастя :)
Колегі-програмісти нагадали, що так робити не під час олімпіади – гріх. Навіть запропонували з таким підходом приєднатися до написання прекрасного AceLewis-калькулятора. До речі, хто не в курсі, що це таке, дуже раджу ознайомитися, скоріше за все ви, як це побачите, то не забудете ніколи.
Чудовий в своєму різноманітті інструментарію Python дозволяє чудово форматувати текст при виводі. Нам треба вирівняти текст вправо в межах двох символів? Не проблема. Як просто і елегантно, правда?
n = int(input())
for x in range(1, n+1):
for y in range(1, n+1):
print(str(x*y).rjust(2), end = ' ')
print()
Округлення, як відомо, це математична операція, яка полягає в заміні числа α наближеним числом α1 із меншою кількістю значущих цифр. Число α1 вибирають так, щоб похибка округлення була якомога меншою.
У різних галузях застосовують різні методи округлення.
На уроках математики в школі традиційно округлюють методом «Округлення до найближчого цілого» (англ. rounding) — це найбільш часто вживаний метод округлення, при якому число округлюється до цілого, модуль різниці з яким у цього числа мінімальний. У загальному випадку, коли число в десятковій системі округляють до N-ого знаку, правило може бути сформульовано таким чином:
якщо N+1 знак < 5, тоді N-ий знак зберігають, а N+1 та всі наступні обнуляють;
якщо N+1 знак ≥ 5, тоді N-ий знак збільшують на одиницю, а N+1 та всі наступні обнуляють;
Наприклад: 11,9 → 12; −0,9 → −1; −1,1 → −1; 2,5 → 3.
Давайте напишемо ще кілька прикладів на даний тип округлення:
Округлюємо до цілого:
1,5 → 2
2,5 → 3
3,5 → 4
4,5 → 5
5,5 → 6
6,5 → 7
Такий метод округлення використовує Python версії 2 і старі програмні компілятори, наприклад Turbo Pascal.
Але це не єдиний метод округлення. Відповідно до стандарту IEEE 754 (і 1985, і 2008 року), основним для комп'ютерних обчислень є інший метод. Він зветься округленням до найближчого парного, банківським, статистичним, данським, Гаусовим округленням. Вважається, що банківське округлення дозволяє зменшити похибки при роботі з великими масивами даних. Подробиці можна дізнатися, завітавши на кілька років на правильну спеціальність гарного університету. Даний метод на сьогодні популярний: наприклад, .NET Math.Round так робить по замовчуванню, цей метод використовує для функції стандартного округлення round() PascalABC.Net і Python 3.
Синтаксично округлення в Python 3 здійснюється функцією round(number, ndigits), де number – число що округлюється, а ndigits - кількість знаків після коми. Наприклад:
>>>round(2.137, 2)
2.14
>>>round(1.5)
2
Ось результат такого округлення:
1,5 → 2
2,5 → 2
3,5 → 4
4,5 → 4
5,5 → 6
6,5 → 6
Саме так округлює функція round() в Python 3.
Але є і великі підводні камені, пов’язані з представленням в пам’яті комп’ютера дійсних чисел. Ось приклад:
>>>round(2.15, 1)
З точки зору округлення до найближчого парного, результат повинен бути 2.2
Python 3 вважає інакше:
>>>round(2.15, 1)
2.1
Це пов’язано з тим, як представлено число 2.15 в машинному поданні, давайте переглянемо, як воно виглядає для, наприклад, 30 знаків після коми:
>>> '%0.30f' % 2.15
'2.149999999999999911182158029987'
Тепер все зрозуміло, в такому випадку логіка округлення Python 3 цілком зрозуміла.
Але сюрпризи при округленні дійсних чисел можуть з’являтися цілком несподівано, наприклад:
>>> round(2.15, 1)
2.1
>>> round(2.1500000000000001, 1)
2.1
>>> round(2.150000000000001, 1)
2.2
Як бачимо, камінців вистачає. Але round() – не єдина функція округлення.
В Python 3, в модулі math реалізовано ще декілька методів округлення:
math.ceil(x) – округлення до найближчого більшого числа
math.floor(x) - округлення до найближчого меншого числа
math.trunc(x) - усікає значення X до цілого.
Ось приклади, що ілюструють роботу даних функцій:
>>> import math
>>> math.ceil(1.4)
2
>>> math.floor(1.4)
1
>>> math.trunc(1.4)
1
>>> math.trunc(1.9)
1
>>> math.floor(-1.9)
-2
>>> math.trunc(-1.9)
-1
Усікти значення до цілого можна і без використання модуля math:
>>> int(1.1)
1
>>> int(1.9)
1
>>> int(-1.1)
-1
>>> int(-1.9)
-1
А для естетів, перфекціоністів, тих, хто хоче забезпечити абсолютну точність, контролювати стратегію округлення і системно керувати золотою рибкою, Python 3 має модуль decimal
Цей неймовірний інструмент має аж вісім варіантів округлення:
ROUND_CEILING - Округлення в сторону позитивної нескінченності. Наприклад, число 2.52 буде округлено до 2.6, а число -2.58 до -2.5
ROUND_DOWN - Округлення в сторону нуля. Наприклад, число 2.58 буде округлено до 2.5, а число -2.58 - до -2.5
ROUND_FLOOR - Округлення в бік негативної нескінченності. Наприклад, число 2.52 буде округлено до 2.5, а число -2.58 до -2.6
ROUND_HALF_DOWN - Округлення в сторону від нуля, якщо частина, що округлюється, більше половини останнього значущого розряду, в іншому випадку округлення буде виконано в сторону нуля. Наприклад, число 2.58 буде округлено до 2.6, число 2.55 буде округлено до 2.5, а число -2.58 до -2.6
ROUND_HALF_EVEN - Те ж, що і ROUND_HALF_DOWN, тільки якщо частина, що округлюється дорівнює точно половині останнього значущого розряду, результат округлюється вниз, якщо попередня цифра парна, і вгору - якщо попередня цифра непарна. Наприклад, число 2.65 буде округлено до 2.6, число 2.55 також буде округлено до 2.6
ROUND_HALF_UP - Те ж, що і ROUND_HALF_DOWN, тільки якщо частина, що округлюється, дорівнює точно половині останнього значущого розряду, результат округлюється в бік від нуля. Наприклад, число 2.55 буде округлено до 2.6, а число -2.55 до -2.6
ROUND_UP - Округлення в бік від нуля. Наприклад, число 2.52 буде округлено до 2.6, а число -2.52 - до -2.6
ROUND_05UP - Округлення в бік від нуля, якщо останній значущий розряд містить цифру 0 або 5, в іншому випадку округлення виконується в сторону нуля. Наприклад, число 2.54 буде округлено до 2.6, число 2.64 також буде округлено до 2.6
Звичайно, всі ці варіанти з’явилися в decimal не просто так - вони мають цілком прикладний сенс. З таким інструментарієм можна реалізувати багато чого, в тому числі і популярне шкільне округлення методом «Округлення до найближчого цілого»:
import decimal as decimal
print(decimal.Decimal('2.5').quantize(decimal.Decimal('1'), rounding=decimal.ROUND_HALF_UP))
print(decimal.Decimal('3.5').quantize(decimal.Decimal('1'), rounding=decimal.ROUND_HALF_UP))
out:
3
4
Ну і можна, звичайно, написати і власну функцію округлення, якщо на то є причини. В будь-якому варіанті тема округлення дійсних чисел в Python 3 має чимало непростих аспектів. І програмістам необхідно уважно враховувати дані особливості як на етапі проектування інформаційних систем, так і при розробці стратегій їх тестування.
Розберемо задачу 8358 з e-olymp. Джерело задачі — 2018 Azerbaijan School Competition, II Stage, April 8, Problem K. На e-olimp на дату написання статті задача опублікована лише російською, тому перекладаю сам:
Середнє значення – 1
(https://www.e-olymp.com/uk/problems/8358)
Проект "Середня вага школяра школи" вирішили виконати Мамед з Самедом. Що вони будуть робити з цим числом, вони не розкривають. Вони попросили зважитися всіх учнів школи і занесли результати в таблицю. Допоможіть їм підрахувати середню вагу учнів. Але вони просять, щоб учнів з найбільшою і з найменшим вагою не враховувати. Єдине їх упущення, вони не підрахували загальну кількість учнів, але це, звичайно, не завадить вам підрахувати то, що вони просять.
Вхідні дані
У кількох рядках задані ваги учнів в кілограмах, розділених пропусками (одним або кількома) або символом кінця рядка. Читати ваги учнів до кінця введення.
Вихідні дані
Середня вага учнів школи без урахування учнів з найбільшою і найменшою вагою. Відповідь виводити з точністю до кілограм.
Ліміт часу 1 секунда
Ліміт використання пам'яті 128 MB
Вхідні дані # 1
40 23 27
59 68 23 84 27
53 46
Вихідні дані # 1
46
В першу чергу треба врахувати, що через невідому кількість рядків вхідних даних, єдиним способом отримати вхідні дані – це використати введення з файлу. Будемо читати рядки з файлу до тих пір, поки не закінчиться файл. Пропоную кожний рядок вхідних даних записувати в тимчасовий список, а далі елементи цього тимчасового списку додавати до основного списку. Код цієї частини програми:
inputfile = open('input.txt', 'r')
outputfile = open('output.txt', 'w')
weights = []
for line in inputfile:
lst = [int(x) for x in line.split()]
weights.extend(lst)
Далі ми можемо використати list comprehension з умовою, наприклад, так ефектно:
weights = [x for x in weights if x != max(weights) and x != min(weights)]
В результаті в новому списку weights будуть лише потрібні дані, всі максимальні і мінімальні ваги в новий список weights не попадуть. Але так робити не треба, тому що це неоптимально по часу і непрофесійно на співбесіді на роботу. Річ в тому, що при кожній ітерації циклу, проходить порівняння значення елементу списку з максимальним і мінімальним елементом списку. І кожного разу python буде обраховувати максимальне і мінімальне значення. Так як список у нас протягом обробки циклом не змінюється, то буде правильним визничити максимальне і мінімальне значення списку до циклічного перебору:
max_weights = max(weights)
min_weights = min(weights)
weights = [x for x in weights if x != max_weights and x != min_weights]
Зверніть увагу на інформативність змінних. В олімпіадному програмуванні часто поспішають і так змінні не називають, а дарма. Рекомендую назви змінним давати розумно, у професійному програмуванню так і роблять.
Ну і на останок, в умові задачі є округлення, це в Python дуже дискутивна тема. Як мінімум, нагадаю, що Python версії 2 виконує так зване «арифметичне округлення», як Pascal, C++ і як на уроках математики, а Python версії 3 при використанні функції round() виконує так зване «банківське округлення» або «округлення до парного». В даній задачі тести обрані таким чином, що при здачі в Python версії 3 ніяких проблем немає, про округлення в Python 3 на «Плетиві» буде окрема стаття, а тим, хто про дива округлення чує вперше, банківське округлення в Python 3 (і не лише там) виглядає так:
>>> round(1.5)
2
>>> round(2.5)
2
>>> round(3.5)
4
>>> round(4.5)
4
>>> round(5.5)
6
>>> round(6.5)
6
>>> round(7.5)
8
>>> round(8.5)
8
І не забувайте прибиратися після себе. Принцип простий. Ви відкрили якийсь файли? Ви відкрили, вам і закривати.
Документація третього Python вимагає так:
If you’re not using the with keyword, then you should call f.close() to close the file and immediately free up any system resources used by it. If you don’t explicitly close a file, Python’s garbage collector will eventually destroy the object and close the open file for you, but the file may stay open for a while. Another risk is that different Python implementations will do this clean-up at different times.
Успіхів!
Розбираємо задачу.
https://www.e-olymp.com/uk/problems/7670
Сьогодні Степан чекає в гості свого друга Василя. Щоб підготуватися до зустрічі, Степану необхідно відвідати два магазини, розташованих поряд з його будинком.
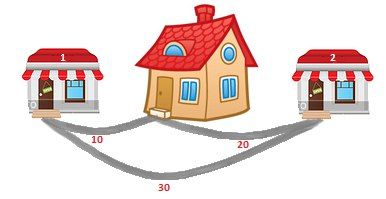
Від будинку до першого магазину веде доріжка довжини d1 метрів, а до другого магазину веде доріжка довжини d2 метри. Також існує доріжка, яка безпосередньо сполучає два магазини один з одним, довжиною d3 метри.
Допоможіть Степану обчислити мінімальну відстань, яку йому буде потрібно пройти, щоб відвідати обидва магазини і повернутися додому.
Степан завжди стартує зі свого будинку. Він повинен відвідати обидва магазини, переміщаючись тільки за наявними трьома доріжками, і повернутися назад додому. При цьому його абсолютно не бентежить, якщо йому доведеться відвідати один і той же магазин або пройти по одній і тій же доріжці більше одного разу. Єдине його завдання - мінімізувати сумарну пройдену відстань.
Вхідні дані
У першому рядку вхідних даних знаходяться 3 цілих числа d1, d2, d3(1 ≤ d1, d2, d3 ≤ 108) - довжини доріжок.
d1 - довжина доріжки, що з'єднує будинок Степана і перший магазин;
d2 - довжина доріжки, що з'єднує будинок Степана і другий магазин;
d3 - довжина доріжки, що з'єднує два магазина.
Вихідні дані
Виведіть мінімальну кількість метрів, яку доведеться пройти Степану, щоб відвідати обидва магазини і повернутися додому.
Ліміт часу 0.1 секунда
Ліміт використання пам'яті 64 MiB
Джерело ACM-ICPC Ukraine 2016, Перший етап Україна, 16 квітня 2016 року
Прекрасна задача на логіку. Давайте спочатку розберем, як взагалі може ходити Степан. Розпишемо всі його можливі маршрути:
Отже - перший машрут. Це коли Степан йде по колу. Тоді відстань буде d1+d3+d2.
Якщо він іде по колу, але в зворотньому напрямку, то його шлях буде d2+d3+d1.
Так як при обох цих вариантах відстань буде однаковою, то будемо вважати ці маршрути як один.
Записуємо, перший маршрут ми визначили.
m1 = d1+d3+d2
Давайте подумаємо, як ще може ходити Степан.
Ще один варіант: він може піти в перший магазин, потім повернутися додому, потім піти в другий магазин і знову повернутися додому.
Записуємо цей маршрут:
m2 = d1+d1+d2+d2
Можна математично гарно це записати:
m2 = (d1+d2)*2
Наступний варіант:
Степан іде в перший магазин, потім в другий магазин. І повертається назад тією ж дорогою.
Записуємо цей маршрут:
m3 = d1+d3+d3+d1
Можна математично гарно це записати:
m3 = (d1+d3)*2
І останній варіант:
Степан іде в другий магазин, потім в перший магазин. І повертається назад тією ж дорогою.
Записуємо цей маршрут:
m4 = d2+d3+d3+d2
Можна математично гарно це записати:
m4 = (d2+d3)*2
В результаті аналізу ми сформували чотири маршрути.
Нам треба визначити найменший.
Відповідна функція python вміє шукати найменше серед і елементів списку і просто змінних:
result = min(m1,m2,m3,m4)
Що нам допомогло розв'язати задачу? Звичайний аналіз і малюнок.
Успіхів!


